

Prepared for Prof. Javed I. Khan
Department of Computer Science, Kent State University
Date: May2004
Computer software is decidedly one of the most complex structures created by mankind for a number of reasons. First and foremostablt, it is a logical structure with no physical representation. As such software does not correspond to many other structures found in the natural world. Second, the number and diversity of interactions between components are limiting factors on any attempt at total system comprehension. These factors make the development, maintenance, testing, comprehension, and management of software a costly and time-consuming activity.
Despite advances in software design techniques, programming languages, and maintenance tools we understand little about the macroscopic structure of software. Most advances in these areas focus on aspects of construction related to software engineering principles first described in the early 1960?s: abstraction, information hiding, and modularity. For example, design technologies and processes such as UML [Fowler'00] and Model Driven Architecture (MDA)[2] advocate techniques that seek to maximize these properties of software via object-oriented programming. Design patterns [Gamma'95] have been proposed to capture solutions to recurring design problems as proven methods for capturing these properties.
The evolution of C-like programming languages has ultimately lead to the realization of these object-oriented properties and is now extending them with model or domain-specific features such as synchronization primitives and embedded database query syntax (most notably, C#).
Research in software maintenance and evolution tends to reconstruct these modular structures to enable a number of maintenance-specific tasks. For example, numerous mental models and approaches to assisted program comprehension have been proposed and implemented along these lines. From a code perspective, automated refactoring tools allow programmers to restructure software to match these object-oriented principles.
Little attention is paid, however to the overall structure and interaction of these components. This is largely due to the size of the data sets in source code. While these applications seek to reduce or better organize the data for better human consumption, they do not focus on the structure of the system as a whole. In this paper we analyze properties of software systems in order to gain some perspective on the overarching structures and trends of the software. Specifically, we extract type dependency graphs from the system and analyze them as large networks. The results of these analyses confirm that some aspects of software systems appear to be similar to social and engineered networks (e.g., the Internet).
This paper is organized as follows: in Section 2, we present related work on the statistical analysis of software. Section 3 describes the methodology of this empirical study. Section 4 presents the results of the analysis. In Section 5, we discuss the results of the findings and their implications on software and development. Finally, in Section 6, we conclude with final thoughts and potential avenues for future research.
As large network analysis (specifically social network analysis) has become an increasingly researched and studied topic, it is inevitable that researchers would eventually start to study software in similar ways. A number of different studies show that software does indeed exhibit properties similar to typical social networks. This is to say they exhibit small-world and scale-free properties.
One of the earliest network analyses of software was presented inn [Valverde'02]. This seminal work shows the first evidence that software is similar to social networks. This work shows that the degrees of classes in a UML diagram follow a power-law distribution (implying scale-free). Additional work in [Valverde'03] shows that the distributions of the in and out-degrees of these diagrams are asymmetric. Specifically, the in-degree distribution admits follows a power-law distribution, while out-degree distributions appear to admit exponential distributions.
A more recent study, [Baxter'06] studies the distributions of a number of structural metrics on Java software. Many of the measures (i.e., those corresponding to the in-degree of classes) also admit power-law distributions. Measures corresponding to the out-degree appear exponential distributions. A similar study [Puppin'06] of roughly 50,000 Java classes also shows that the in-degree of classes models a scale-free network. This information was used to help build a Pagerank-like Page'98] portal for searching Java software. A study by [Myers'03] describes the out-degree of some systems as also admitting a power-law distribution. However, this may be misreported due to smaller data sets.
In [Potanin'05] a similar analysis is applied to object graphs of Java programs obtained via runtime analysis. Interestingly, object graphs (as opposed to the more frequently studied class or dependency graphs above) also exhibit scale-free properties.
This section describes the empirical methods used to perform this study. Specifically, we describe our definition of type dependency graphs, the method for extracting and analyzing them, and the different software projects to which the analyses are applied.
In this work, we are interested in studying the accumulated type dependency graphs of C++ systems. These software graphs differ from the graphs studied in [Baxter'06, Myers'03, Puppin'06, Valverde'02, '03] in that they incorporate significantly more information into the graph. We define a type dependency graph as a directed graph:
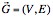
where V is the set of all classes in a software system and E is the set of edges denoting type dependency. A type dependency exists if and only if a class A requires another class B to function properly. This is to say that A depends on B if any one of the following conditions is satisfied
Note that in this analysis, edges are unweighted. Moreover, multiple references between class A and B will only contribute a single edge instead of multiple links between classes.
The last condition is used to cover the case where class A contains instances of B transitively via a template container or smart pointer. Template classes and their instances are not included in the analysis. Templates are not actually classes, and instances of template classes will simply duplicate the analysis results for every different combination of arguments used during instantiation. We suspect that this would skew the results in an unpredictable way.
Type dependency graphs extracted from software systems by the pilfer reverse engineering system [Sutton'05a, '05b]. pilfer uses srcML[3] technology [Collard'03, '02, Maletic'02] to create a lexical markup of the C++ source code. This markup is used as the basis for the pilfer syntactic and semantic analysis engines to create an in-memory model of the C++ program. A program src2tdg uses the resulting model to produce a GraphViz-compatible graph description[4].
Once the GraphViz files have been produced describing the type dependency graphs, a set of simple graph analysis tools were built to compute graph and network metrics. These tools all use the Boost Graph Library[5] to load the graph and compute degree distributions and mean geodesic distances. A set of Python scripts were then built to compute various distributions and histograms. The architecture and workflow of the application are shown in Figure 1.
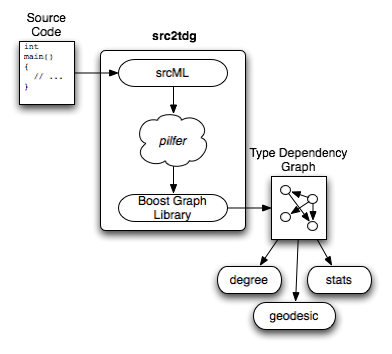 |
| Figure 1. The src2tdg workflow. Source code is parsed into srcML, reverse engineered with pilfer, serialized as a GraphViz file. Additional tools are used to extract and create statistics from the resultant graphs. |
We analyzed five different software systems in this work: HippoDraw, the Open Modeling Framework (OMF) , Ogre, Qt, and the KDE core libraries (kdelibs). HippoDraw[6] is an information visualization tool developed by SLAC. The Open Modeling Framework[7] is a library that implements the Meta-Object Facility (MOF) and Unified Modeling Language (UML) metamodels. Ogre[8] is a library and framework for developing 3d applications. Qt[9] is platform independent library for developing windowed applications, and kdelibs[10] is the core infrastructure for the KDE Desktop Environment. For each of these programs, we produced and analyzed the degree distributions and mean geodesic distance. Basic statistics for each of these applications are given in Table 1.
| N | L | KLOC | |
|---|---|---|---|
| HippoDraw | 298 | 1371 | 104 |
| OMF | 482 | 1581 | 61 |
| Ogre | 770 | 2966 | 230 |
| Qt | 1876 | 8707 | 1044 |
| KDE Libs | 3369 | 14876 | 921 |
Together 5 systems represent a total of 6795 classes and roughly 2.3 MLOC (million lines of code).
We analyzed the above software systems for a couple of different properties ? namely their mean geodesic distance and their degree distributions. Specifically, we want to show (or not show) that type dependency graphs are similar to social networks, or that they exhibit the small-world or scale-free properties.
The first aspect of type dependency graphs we want to look at is whether or not they exhibit a small-world property. To do this, we computed the mean geodesic distance for each system. We define the mean geodesic distance as:
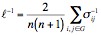
where sij denotes the geodesic distance (shortest path) between classes i and j in the software system. Intuitively, the mean geodesic distance determines the average number of hops to get from one node to another in the graph. The small-world property exists for graphs with a low (usually less than 10) mean geodesic distance. Although there are number of different ways to compute the mean geodesic distance [Newman'03], we chose this definition because many of the software systems are comprised of numerous unconnected components.
The results of this analysis (shown in Table 2) were surprising. Contrary to the results reported in [Valverde'03], we did not find the small-world property exhibited many of these systems - certainly not consistently. The reason for this is that the metric is computed over a directed graph.
When we computed the mean geodesic distance over the underlying undirected graph, we get results similar to those reported in the literature.
| Directed | Undirected | |
|---|---|---|
| HippoDraw | 12.94 | 1.56 |
| OMF | 13.48 | 1.64 |
| Ogre | 9.47 | 1.84 |
| Qt | 19.95 | 2.06 |
| KDE Libs | 41.48 | 1.66 |
These results are intriguing. The graphs examined in the surveyed literature are all directed graphs, and the type dependency graph is no different. In order to show a small-world property for these graphs, we have to treat them as undirected graphs ? which software is most certainly not. In many cases treating these graphs as undirected disregards the original semantics or intent of the graph representation. In the case of type dependency graphs, considering undirected edges introduces an implication that a class ?knows? the classes that use it. As C++ type references are made without a referencing context, this computation is inconsistent with the semantics of the original graph.
The in-degree of structural software graphs such as the type dependency corresponds to the number of times a class is used (reused) in many cases. In short, a reusable class encapsulates some functionality that others find useful. During our initial analysis of the in-degree distributions, it quickly became apparent that these graphs were admitting power-law distributions in their in degrees. The distributions of the in-degree of the analyzed systems are shown in Figure 2.
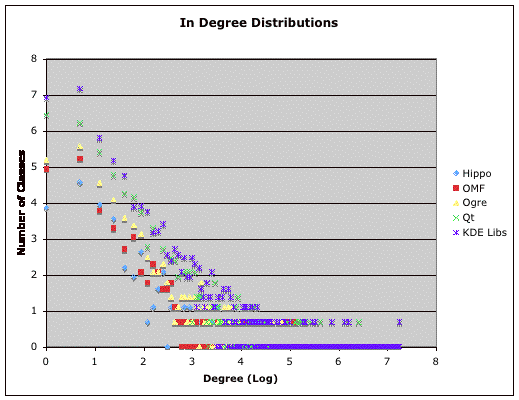 |
| Figure 2. The distribution of in-degrees in a log-log plot. |
However, we wanted to approximate the actual distribution that these graphs are being generated from. We hypothesize that these are coming from a Pareto distribution. Remember that a power-law distribution is given by the probability distribution function:
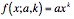
where a is location parameter and k is a scaling parameter with k <e; 0 (usually). As stated, we had originally hypothesized that these distributions are actually instances of a Pareto distribution. However, the Pareto distribution is given by the probability distribution function:
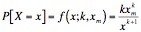
where xm is the minimum observed value and k is a scaling factor. The cumulative distribution function is given by the function:
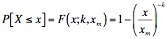
Note, however, that neither distribution fits the power-law function given above. However, we can consider alternative probability distributions of the Pareto distribution. Specifically, we consider the case where X is a random variable such that X ~ Pareto(k, xm), then
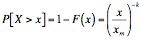
When xm is 1, this becomes exactly a power-law distribution. In order to determine if the type dependency graphs admit Pareto distributions, we must show a similar function for the same probability distribution. In order to generate this distribution, we generated the probability distribution for the histogram in Figure 2. By cumulating the probabilities from right to left, we ended up with the function given above - namely, a distribution giving P[X > x] for the in-degree of the type dependency graphs. We call this the inverse cumulative distribution function.
In order to plot these, we computed expected values for the probabilities in the inverse cumulative distribution function by multiplying each probability by the number of classes in the distribution. These results are binned logarithmically in order to smooth the long tail typically present in power-law distributions. The results are shown in Figure 3.
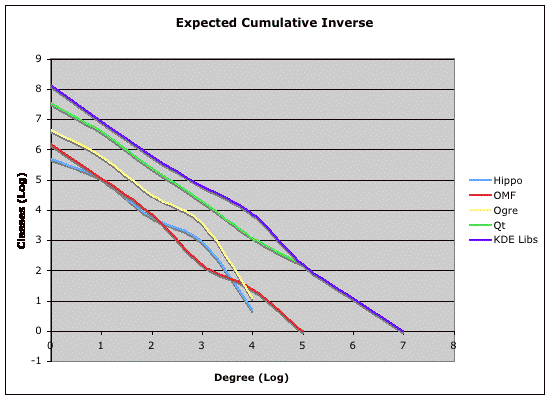 |
| Figure 3. The inverse cumulative distribution of in-degrees, binned logarithmically and plotted against a logarithmic scale. |
It is convenient that power-law curves will always appear as lines on log-log plots, and the slopes of those lines correspond to the the scaling factor k in the power-law function. Because these curves are all approximately lines on this plot, we can safely surmise that these are power-law functions derived from the probability function P[X > x]. This implies that these distributions are instances of a Pareto distribution with a scaling factor k. We used affine interpolation to approximate the slope of the lines in Figure 3. This yields the following results:
| k | |
|---|---|
| HippoDraw | 1.39 |
| OMF | 1.26 |
| Ogre | 1.50 |
| Qt | 1.09 |
| KDE Libs | 1.16 |
These results are consistent with the results reported in previous literature. However, because we have shown that these model a Pareto distribution, we can derive other general observations ? specifically observations about the mean and variance of the distributions. The mean of a Pareto distribution is given as:
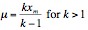
Again, taking xm as 1, this results in relatively low means. Interestingly, the mean in-degree for all analyzed graphs tends to also be quite low ? in the range 3 to 5 ? which is nicely approximated by the Pareto mean. Also interesting is the variance of a Pareto distribution, which is given as:
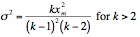
If the scaling factor is less than 2, then the distribution has an infinite variance. It is immediately obvious (and quite intriguing) that the scaling factors for the given distributions meet this criteria - their in-degrees are all infinitely varied.
In the research literature, the out-degree of these distributions is typically given only passing treatment. As the reported out-degree distributions do not appear to follow a power-law distribution, they appear to be less interesting to the authors.
We perform the same analysis for the out-degree distributions that we do for the in-degree distributions. Namely, we derive the inverse cumulative distribution for out-degree. The results are shown in Figure 4. It is quite apparent that the out degrees of these distributions are distinctly not power-law distributions. In fact, they appear to decay exponentially, suggesting an exponential distribution.
Unfortunately, we cannot yet show that these are, in fact, instances of exponential distributions, neither has this been shown in the research literature. However, there is evidence to support the claim (namely the shape of the curves in Figure 4).
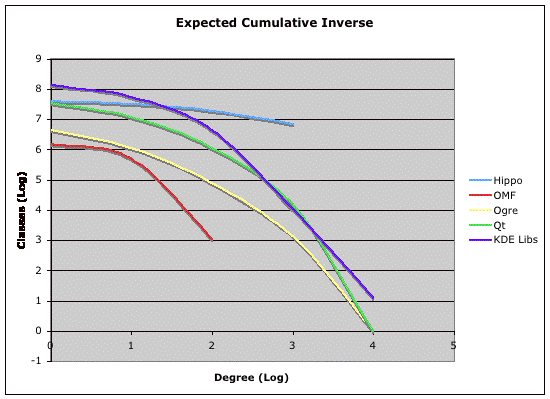 |
| Figure 4. The inverse cumulative distributions of out-degrees, binned logarithmically and plotted against a logarithmic scale. |
The exponential distribution is given by the probability distribution function:
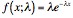
Exponential distributions are typically given with by the rate parameter l and are typically used to describe conditions in time-series or rate-based analyses (e.g., failure rates or packet inter-arrival times). However, this is difficult to conceptually map this onto software systems since the graphs are in no way rate-based. In short, it is difficult to ascertain the significance of exponential distributions governing the occurrence of out-degrees in software systems.
If these truly are exponential distributions, then we can derive the rate l using the distribution's mean. The mean of the exponential distribution is given by:
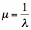
Therefore, knowing the mean of the out-degree distributions will allow us to approximate the means. The mean out-degree and rate for this distribution is given are given in Table 4.
| Mean | Rate | |
|---|---|---|
| HippoDraw | 4.60 | 0.21 |
| OMF | 3.23 | 0.31 |
| Ogre | 3.85 | 0.25 |
| Qt | 4.64 | 0.22 |
| KDE Libs | 4.41 | 0.23 |
These rates appear to match the curves in Figure 4 quite well as they all exhibit a relatively slow tapering toward zero. However, support for this distribution fit would be improved with larger samples or by the application of statistical goodness-of-fit tests.
There are several results of interest in this empirical study of software. More interesting are some of the implications arising from the results.
First, the mean geodesic distance of these graphs do not necessarily show proof of a small-world property, (specifically in the case of this values computation on the directed type dependency graphs). However, the Ogre 3D library does appear to exhibit the small-world property in it?s directed graph. This is an interesting (and apparently atypical) case of system design, and the only way to show this property for a directed graph is to have a high degree of reflexive connections between classes. This is to say that the back-pointer or back-reference idiom is a common occurrence (i.e., parent/child relationships) ? which appears to be the case for Ogre.
One aspect worth investigating is whether or not this type of reflexive coupling affects the maintainability of a software system. We might guess that it makes the system more difficult to maintain since changes in one class must often be reflected to other classes due to the extensive coupling via back-pointers. It would be worth investigating whether or not the mean geodesic distance of a directed type dependency graph provides an accurate predictor for maintenance cost.
When looking at the results of the mean geodesic distance for undirected graphs, we see that these distances are very low ? much lower in fact than typical social or engineered networks [Newman'03]. The reason for this is not too surprising. It turns out that most systems employ a small number of classes that are used by virtually all others. These classes are almost all primitive aggregate types (e.g., string, complex, point, rectangle, etc). or abstract data types (e.g., list, vector, dictionary, etc.). Had we included the use of language specific primitive types (e.g., int, float, etc.), we would have seen even lower mean geodesic distances and a much longer tail than shown in the degree distributions.
This widespread use of datatypes is ultimately responsible for the small-world property of undirected type dependency graphs. However, this is a purely incidental result and has little real impact in the actual analysis, testing, or comprehension of software systems. This is due to the fact that the graphs being analyzed are not undirected ? which seems to be a common assumption in the computation of this metric. However, as a whole, the (very) low mean geodesic distance shows that the system designers (and programmers) are following good practices and reusing software components. On the other hand, it is difficult to think of classes that do not, in some way, depend on some primitive or commonly reused abstract data type.
An alternative analysis of degree distributions might well involve ignoring results for such highly reused classes. As a class becomes ubiquitous in its use, should we treat it as part of the system or part of the language?
Remembering that in-degree corresponds (roughly) to a measure of reuse in a software system, finding an infinite variance is surprising. The implication is simple: a developer can expect to have a relatively low average reusability factor, but cannot predict whether or not the class will actually be reused to any great degree. This evidence is supported when looking at the mean and variance of the actual systems. For example, the mean in-degree of kdelibs is only 4.42 incoming edges, but the variance of that sample is a striking 919.52. Similar measures can be found for the other systems. While there is no perfect trend, we can hypothesize that the variance of these degrees will grow asymptotically with the size of the system.
The inability to predict the reusability of a class is a serious detriment to reuse testing strategies. Ideally, we would want to test classes more thoroughly if they are frequently reused. A flaw in one of these classes will have significant ripple-effect, most likely causing total program failure. Because the amount of reuse cannot be determined without first analyzing the entire system, it is impossible to predict (without some apriori knowledge) which classes should be tested.
One of the most striking results of this study is the evidence of a Pareto distribution that governs the occurrence of in-degrees in type dependency graphs. Although this evidence is well supported in previous literature, little mention is given as to why this should be so. Remember that incoming edges to classes imply that the class is most likely being reused. The classes with the highest level of reuse in many of these systems turn out to be simple datatypes such as strings or abstract data types. The one exception to the rule is the OMF where the most reused object is the OMF::ModelObject class. However, the OMF is essentially a collection of simple data types where the most of the classes in the library are derived from the aforementioned class.
The fact that the distribution of in-degrees follows a power-law distribution provides evidence of scale-free network. Power-law distributions are commonly associated with scale-free networks. A function is said to be scale-free if it satisfies the following property:
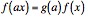
Intuitively, this states that an increase by a factor a in the scale of x will not change the density of f except by a multiplicative scaling factor. The only functions that are scale-free in this sense are power-law distributions. However, this notion of ?scale-free? is insufficient in its application to discrete topologies. In [Li'05], a metric s(g) is defined as a structural measure of an undirected graph g as the extent to which said graph is scale-free. It is given as:
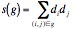
where di is the degree of node i. Intuitively, this computes a degree weight for each edge (i, j) in the graph g. Graphs (or networks) are said to be scale-free if their s value is high. However, this metric (much like the mean geodesic distance) is computed on the undirected graph. Although this violates the semantics of the original graph, it does help establish a measure of connectedness. Computations of this value for the given software systems show them to have s values between 640 thousand (HippoDraw) and 38 million (kdelibs). These seem to be fairly high values, supporting the notion that these are all scale-free graphs.
Additionally, [Li'05] identifies six different properties of scale-free networks. Specifically that scale-free networks:
We have already shown (claim 1) that software has a power-law in-degree distribution. It is also likely that the cumulative degree distribution admits a power-law distribution.
In terms of their in-degree software certainly does exhibit a hub-like structure (claim 3). The hubs, in the case of software system, are reusable data structures and abstract data types. Classes not directly connected to these ?hubs? will almost certainly delegate or be related to other classes that are.
Claims 2 and 4 are of great interest to people studying the processes of software development and evolution. One of the more interesting questions posed is whether or not software is the outcome of various random growth properties. To verify this, we have to look at the development processes that contribute to the construction of software. The number of factors influencing the development and evolution of software are innumerable so we might guess that the interacting forces and requirements produce such processes. Moreover, is it possible to look at incremental changes to software as a "degree-preserving rewiring process" It seems unlikely since software changes do not arbitrarily shuffle dependencies between classes. Interestingly, the basic nature of stochastic processes used to generate such graphs require incremental grow (classes added one or a few at a time) and preferential attachment (reuse of existing classes is preferred). Although the theoretical process for evolving software is unknown, these two properties are an ideal for software construction. Consider an alternative in which many classes are added simultaneously by different developers. This could lead to situations where functionality is duplicated, making the software less maintainable. This trivial scenario gives a strong argument for even marginal up-front design.
We have shown that claim 5 also holds with software. The projects we have chosen represent different domains and sub-domains. This is to say that each implements different, sometimes unrelated, concerns from various application domains. This implies that software will form scale-free networks (of reuse) regardless of problem domain, implementation domain, programming language, reuse libraries, or even design patterns.
Finally, software reuse is ?self-similar?. Self-similarity is a term often applied to functions, geographies or topologies of a fractal nature. Whether or not software systems exhibit a fractal-like quality is an open question. However, based on the definitions of ?scale-free? and its associated properties, it does indeed appear that software is (at least partially) fractal - especially in its reuse. It is not too hard to imagine dense clusters of classes surrounding ubiquitous types. Inside these clusters are smaller domain-specific clusters around domain-specific data types. If software reuse is truly self-similar than this pattern of domain-clustered reuse will persist even as the clusters grow smaller and smaller.
In this work, we have analyzed three different properties of a number of software systems: the mean geodesic distance and both in and out-degree distributions. Specifically, we have examined these properties of type dependency graphs that have been extracted using our software pilfer.
Resulting analysis has shown that the undirected graphs of these systems do exhibit the small-world property, while it is much less likely for their directed variants to do so. Moreover, we have given convincing evidence that the reuse (in-degree) of classes admits a Pareto distribution. This has lead to the observation that software reuse is completely unpredictable due to the infinite variance of the in-degree. Finally, we have observed that the design (out-degree) of classes appears to follow an exponential distribution but have given no solid evidence nor been able to determine the significance.
An extension of this work would be to study different relationships separately. This work, for example studies a cumulative type dependency graph that ignores the semantics of relationships between classes. One possible extension to this work would be to study the structure of software along specific relationships. For example, inheritance is different than aggregation (member variables), and both are distinct from incidental dependencies such as parameter types, return types, and local variable types. The work in [Baxter'06] studies these relationships separately and observes similar properties in each of them.
Another possible and promising direction would be to perform an analysis of the system over time. This would require ?replaying? the development and evolution of a software system and measuring its properties over time. Specifically, we could examine the size, complexity and arrival times of changes to the system and the impact those changes have on the structure of the system. This analysis could provide a statistical model for the growth and evolution of software systems.
This work, like those before, only serves to inspire additional questions about the structure of software and potentially leads to a great deal of future work. Clearly, one such work would be to validate that the out-degrees of distributions are exponentially distributed, and if they are what significance that has on the structure of software. The greatest challenge of this venue of research is to show that it is beyond theoretical interest and has practical applications. This can only be done by showing that the results shown here and established in prior studies have some practical application in software engineering.
We believe that this work may have applications in software reuse measures, program comprehension and impact analysis. The results from the analysis of software reuse show a marked tendency toward self-similarity. Extrapolating this, we might envision the distribution as a quantitative measure of effective reuse. Because the rules for growing these graphs are dependent upon the rules of incremental growth and preferential attachment, any deviation from this process could negatively impact the quality of the software. Specifically, such a measure might indicate poor design decisions and significant duplication of functionality.
Graphs exhibiting these properties have already been exploited in different applications. For example, the Pagerank algorithm is designed to work with similar datasets, returning the most "popular" websites. A similar approach could be taken for software, allowing users to search for concepts in software based on the ?popularity? of different systems Puppin'06].
Impact analysis, used frequently in testing scenarios may also benefit from applications of these theoretical results. The patterns of inter-connectedness of software type dependencies may help drive the development of algorithms for determining the maximal or minimal impact of a change to a software system.
In general, the theoretical results described in this work may help drive the development or improvement of a number of different algorithms for automated software engineering. Understanding the structure or properties of graphs is fundamental to the development or optimization of algorithms, and we see no reason why applications in software engineering would not benefit from a similar analysis.
Ultimately, we hope that this research will result in the development for a theoretical model for the structure and evolution of software systems. Such a model could help software engineers better understand the interactions between the process and the product. Moreover, a model may provide the means for more accurate and meaningful measures of software complexity and quality [Pfleeger'97].
| [Baxter'06] | Baxter, G., Frean, M., Noble, J., Rickerby, M., Smith, H., Visser, M., Melton, H., and Tempero, E., (2006), "Understanding the Shape of Java Software", in Proceedings of ACM SIGPLAN Object Oriented Systems, Languages, and Applications, Portland, Oregon, October 22-26, pp. (Submitted). |
| [Collard'03] | Collard, M. L., Kagdi, H. H., and Maletic, J. I., (2003), "An XML-Based Lightweight C++ Fact Extractor", in Proceedings of 11th IEEE International Workshop on Program Comprehension (IWPC'03), Portland, OR, May 10-11, pp. 134-143. |
| [Collard'02] | Collard, M. L., Maletic, J. I., and Marcus, A., (2002), "Supporting Document and Data Views of Source Code", in Proceedings of ACM Symposium on Document Engineering (DocEng?02), McLean VA, November 8-9, pp. 34-41. |
| [Fowler'00] | Fowler, M., (2000), UML Distilled Third Edition A Brief Guide to the Standard Object Modeling Language, Addison-Wesley. |
| [Gamma'95] | Gamma, E., Helm, R., Johnson, R., and Vlissides, J., (1995), Design Patterns, Addison-Wesley. |
| [Li'05] | Li, L., Alderson, D., Tanaka, R., Doyle, J. C., and Willinger, W., (2005), "Towards a Theory of Scale-Free Graphs: Definitions, Properties, and Implications (Extended Versions)", Arxiv, http://www.citebase.org/cgi-bin/citations?id=oai:arXiv.org:cond-mat/0501169. |
| [Maletic'02] | Maletic, J. I., Collard, M. L., and Marcus, A., (2002), "Source Code Files as Structured Documents", in Proceedings of 10th IEEE International Workshop on Program Comprehension (IWPC'02), Paris, France, June 27-29, pp. 289-292. |
| [Myers'03] | Myers, C. R., (2003), "Software Systems as Complex Networks: Structure, Function, and Evolvability of Software Collaboration Graphs", Physical Review E (Statistical, Nonlinear, and Soft Matter Physics), vol. 68, no. 4, October 2003. |
| [Newman'03] | Newman, M. E. J., (2003), "The Structure and Function of Complex Networks", SIAM Review, vol. 45, no. 2, 2003, pp. 167-256. |
| [Page'98] | Page, L., Brin, S., Motwani, R., and Winograd, T., (1998), "The Pagerank Citation Ranking: Bringing Order to the Web". Stanford, California: Stanford University. |
| [Pfleeger'97] | Pfleeger, S. L., Ross, J., Curtis, B., and Kitchenham, B., (1997), "Status Report on Software Measurement", IEEE Software, vol. 14, no. 2, March/April 1997, pp. 33-43. |
| [Potanin'05] | Potanin, A., Noble, J., Frean, M., and Biddle, R., (2005), "Scale-Free Geometry in OO Programs", ACM Communications, vol. 48, no. 5, May 2005, pp. 99-103. |
| [Puppin'06] | Puppin, D. and Sylvestri, F., (2006), "The Social Network of Java Classes", in Proceedings of 21st ACM Symposium on Applied Computing (SAC'06), Dijon, France, pp. (Submitted). |
| [Sutton'05a] | Sutton, A., (2005), Accurately Reverse Engineering UML Class Models from C++, Kent State University, Kent, Ohio, Masters Thesis. |
| [Sutton'05b] | Sutton, A. and Maletic, J. I., (2005), "Mappings for Accurately Reverse Engineering UML Class Models from C++", in Proceedings of 12th Working Conference on Reverse Engineering (WCRE ' 05), Pittsburgh, PA, Nov 7-11, pp. 175-184. |
| [Valverde'02] | Valverde, S. and Solé, R. V., (2002), "Scale-Free Networks from Optimal Design", Europhysics Letters, vol. 60, no. 4, November 2002, pp. 512-517. |
| [Valverde'03] | Valverde, S. and Solé, R. V., (2003), "Hierarchical Small Worlds in Software Architecture", Arxiv, http://www.citebase.org/cgi-bin/citations?id=oai:arXiv.org:cond-mat/0307278. |